How To Find The Cardinality Of A Set

Number of elements of a prepare

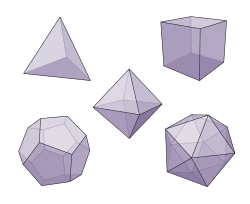
The ready $S$ of all Platonic solids has 5 elements. Thus $|South|=5$ .

In mathematics, the cardinality of a set is a mensurate of the "number of elements" of the prepare. For example, the fix $A=\{two,4,six\}$ contains 3 elements, and therefore $A$ has a cardinality of 3. Beginning in the tardily 19th century, this concept was generalized to space sets, which allows one to distinguish betwixt the different types of infinity, and to perform arithmetic on them. There are 2 approaches to cardinality: 1 which compares sets directly using bijections and injections, and some other which uses cardinal numbers.^[1] The cardinality of a set is likewise called its size, when no defoliation with other notions of size^[ii] is possible.

The cardinality of a set $A$ is usually denoted $|A|$ , with a vertical bar on each side;^[3] this is the same notation every bit absolute value, and the meaning depends on context. The cardinality of a set $A$ may alternatively be denoted by $due north(A)$ , $A$ , $\operatorname {menu} (A)$ , or $\#A$ .

History [edit]

This section needs expansion. You can help by adding to it. (September 2021)

In the 1890s, Georg Cantor generalized the concept of cardinality to space sets,^[4] which allowed one to distinguish betwixt the different types of infinity and to perform arithmetics on them.

Comparing sets [edit]

Bijective office from N to the set E of even numbers. Although E is a proper subset of N, both sets take the same cardinality.

N does not have the same cardinality every bit its ability set P(Northward): For every role f from Northward to P(N), the set T = {north∈Due north: north∉f(north)} disagrees with every set up in the range of f, hence f cannot be surjective. The picture shows an case f and the respective T; ruddy : due north∈f(n)\T, blueish :due north∈T\f(n).

While the cardinality of a finite ready is only the number of its elements, extending the notion to infinite sets usually starts with defining the notion of comparison of capricious sets (some of which are possibly infinite).

Definition 1: | A | = | B | [edit]

Two sets A and B accept the same cardinality if there exists a bijection (a.m.a., ane-to-one correspondence) from A to B,^[v] that is, a function from A to B that is both injective and surjective. Such sets are said to be equipotent, equipollent, or equinumerous. This relationship can likewise be denoted A ≈ B or A ~ B.

For example, the fix East = {0, two, 4, vi, ...} of not-negative even numbers has the same cardinality as the set Due north = {0, 1, 2, iii, ...} of natural numbers, since the role f(due north) = 2due north is a bijection from N to East (see picture).

Definition ii: | A | ≤ | B | [edit]

A has cardinality less than or equal to the cardinality of B, if in that location exists an injective office from A into B.

Definition 3: | A | < | B | [edit]

A has cardinality strictly less than the cardinality of B, if at that place is an injective role, but no bijective function, from A to B.

For case, the gear up N of all natural numbers has cardinality strictly less than its power set P(Northward), because yard(n) = { n } is an injective function from North to P(N), and it can exist shown that no function from N to P(N) tin can be bijective (see pic). By a like statement, N has cardinality strictly less than the cardinality of the gear up R of all existent numbers. For proofs, encounter Cantor's diagonal argument or Cantor's first uncountability proof.

If | A | ≤ | B | and | B | ≤ | A |, and so | A | = | B | (a fact known as Schröder–Bernstein theorem). The axiom of choice is equivalent to the statement that | A | ≤ | B | or | B | ≤ | A | for every A, B.^{[half dozen]} ^[7]

Primal numbers [edit]

In the in a higher place section, "cardinality" of a set was divers functionally. In other words, it was not defined every bit a specific object itself. Still, such an object can exist defined as follows.

The relation of having the aforementioned cardinality is chosen equinumerosity, and this is an equivalence relation on the class of all sets. The equivalence course of a set A nether this relation, then, consists of all those sets which accept the same cardinality every bit A. There are ii ways to define the "cardinality of a set":

The cardinality of a ready A is divers equally its equivalence class under equinumerosity.
A representative set is designated for each equivalence grade. The most mutual selection is the initial ordinal in that class. This is usually taken every bit the definition of cardinal number in axiomatic gear up theory.

Assuming the axiom of choice, the cardinalities of the infinite sets are denoted

\aleph _{0}<\aleph _{i}<\aleph _{2}<\ldots .

For each ordinal $\blastoff$ , $\aleph _{\alpha +1}$ is the least cardinal number greater than $\aleph _{\alpha }$ .

The cardinality of the natural numbers is denoted aleph-null ( $\aleph _{0}$ ), while the cardinality of the real numbers is denoted by " ${\mathfrak {c}}$ " (a lowercase fraktur script "c"), and is too referred to every bit the cardinality of the continuum. Cantor showed, using the diagonal statement, that ${\mathfrak {c}}>\aleph _{0}$ . We can prove that ${\mathfrak {c}}=two^{\aleph _{0}}$ , this also being the cardinality of the set of all subsets of the natural numbers.

The continuum hypothesis says that $\aleph _{i}=ii^{\aleph _{0}}$ , i.east. $2^{\aleph _{0}}$ is the smallest cardinal number bigger than $\aleph _{0}$ , i.e. there is no set whose cardinality is strictly between that of the integers and that of the existent numbers. The continuum hypothesis is independent of ZFC, a standard axiomatization of set theory; that is, it is incommunicable to show the continuum hypothesis or its negation from ZFC—provided that ZFC is consistent. For more detail, see § Cardinality of the continuum below.^[8] ^[9] ^[10]

Finite, countable and uncountable sets [edit]

If the axiom of choice holds, the constabulary of trichotomy holds for cardinality. Thus we can make the following definitions:

Infinite sets [edit]

Our intuition gained from finite sets breaks downwardly when dealing with infinite sets. In the tardily nineteenth century Georg Cantor, Gottlob Frege, Richard Dedekind and others rejected the view that the whole cannot be the same size equally the office.^[11] ^{[ commendation needed ]} Ane example of this is Hilbert's paradox of the Yard Hotel. Indeed, Dedekind defined an space gear up equally 1 that tin can exist placed into a one-to-one correspondence with a strict subset (that is, having the same size in Cantor's sense); this notion of infinity is called Dedekind infinite. Cantor introduced the cardinal numbers, and showed—according to his bijection-based definition of size—that some infinite sets are greater than others. The smallest infinite cardinality is that of the natural numbers ( $\aleph _{0}$ ).

Cardinality of the continuum [edit]

I of Cantor's near important results was that the cardinality of the continuum ( ${\mathfrak {c}}$ ) is greater than that of the natural numbers ( $\aleph _{0}$ ); that is, there are more than real numbers R than natural numbers Northward. Namely, Cantor showed that ${\mathfrak {c}}=ii^{\aleph _{0}}=\beth _{1}$ (see Beth one) satisfies:

2^{\aleph _{0}}>\aleph _{0}

(see Cantor's diagonal argument or Cantor's kickoff uncountability proof).

The continuum hypothesis states that at that place is no cardinal number between the cardinality of the reals and the cardinality of the natural numbers, that is,

2^{\aleph _{0}}=\aleph _{1}

Withal, this hypothesis can neither be proved nor disproved within the widely accepted ZFC evident set up theory, if ZFC is consistent.

Cardinal arithmetic can be used to evidence not only that the number of points in a real number line is equal to the number of points in any segment of that line, but that this is equal to the number of points on a plane and, indeed, in whatever finite-dimensional infinite. These results are highly counterintuitive, because they imply that there exist proper subsets and proper supersets of an infinite set S that have the same size every bit S, although S contains elements that do non belong to its subsets, and the supersets of S comprise elements that are not included in it.

The first of these results is apparent by considering, for case, the tangent function, which provides a one-to-1 correspondence betwixt the interval (−½π, ½π) and R (see as well Hilbert'south paradox of the Grand Hotel).

The second upshot was offset demonstrated past Cantor in 1878, simply it became more apparent in 1890, when Giuseppe Peano introduced the infinite-filling curves, curved lines that twist and turn enough to fill the whole of whatever square, or cube, or hypercube, or finite-dimensional space. These curves are not a directly proof that a line has the same number of points as a finite-dimensional infinite, only they tin can exist used to obtain such a proof.

Cantor likewise showed that sets with cardinality strictly greater than ${\mathfrak {c}}$ exist (meet his generalized diagonal argument and theorem). They include, for instance:

the set of all subsets of R, i.e., the power set of R, written P(R) or 2^R
the set R ^R of all functions from R to R

Both have cardinality

2^{\mathfrak {c}}=\beth _{2}>{\mathfrak {c}}

(encounter Beth two).

The cardinal equalities ${\mathfrak {c}}^{two}={\mathfrak {c}},$ ${\mathfrak {c}}^{\aleph _{0}}={\mathfrak {c}},$ and ${\mathfrak {c}}^{\mathfrak {c}}=ii^{\mathfrak {c}}$ can exist demonstrated using primal arithmetic:

{\mathfrak {c}}^{2}=\left(2^{\aleph _{0}}\correct)^{two}=2^{two\times {\aleph _{0}}}=ii^{\aleph _{0}}={\mathfrak {c}},

{\mathfrak {c}}^{\aleph _{0}}=\left(2^{\aleph _{0}}\right)^{\aleph _{0}}=2^{{\aleph _{0}}\times {\aleph _{0}}}=2^{\aleph _{0}}={\mathfrak {c}},

{\mathfrak {c}}^{\mathfrak {c}}=\left(2^{\aleph _{0}}\right)^{\mathfrak {c}}=2^{{\mathfrak {c}}\times \aleph _{0}}=2^{\mathfrak {c}}.

Examples and properties [edit]

If 10 = {a, b, c} and Y = {apples, oranges, peaches}, then |10 | = |Y | because { (a, apples), (b, oranges), (c, peaches)} is a bijection between the sets X and Y. The cardinality of each of Ten and Y is 3.
If |Ten | ≤ |Y |, so there exists Z such that |X | = |Z | and Z ⊆ Y.
If |X | ≤ |Y | and |Y | ≤ |10 |, then |10 | = |Y |. This holds even for infinite cardinals, and is known as Cantor–Bernstein–Schroeder theorem.
Sets with cardinality of the continuum include the set of all existent numbers, the set of all irrational numbers and the interval $[0,1]$ .

Union and intersection [edit]

If A and B are disjoint sets, and then

\left\vert A\cup B\correct\vert =\left\vert A\right\vert +\left\vert B\right\vert .

From this, one can bear witness that in general, the cardinalities of unions and intersections are related past the following equation:^[12]

\left\vert C\cup D\right\vert +\left\vert C\cap D\right\vert =\left\vert C\right\vert +\left\vert D\right\vert .

See too [edit]

Aleph number
Beth number
Cantor'due south paradox
Cantor's theorem
Countable gear up
Counting
Ordinality
Pigeonhole principle

References [edit]

^ Weisstein, Eric Westward. "Cardinal Number". MathWorld.
^ Such as length and surface area in geometry. – A line of finite length is a set of points that has infinite cardinality.
^ "Cardinality | Brilliant Math & Science Wiki". brilliant.org . Retrieved 2020-08-23 .
^ The Princeton Companion to Mathematics. Princeton Academy Press. 2008. p. 779.
^ ^a ^b "Infinite Sets and Cardinality". Mathematics LibreTexts. 2019-12-05. Retrieved 2020-08-23 .
^ Friedrich Yard. Hartogs (1915), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Über das Problem der Wohlordnung", Mathematische Annalen, Leipzig: B. G. Teubner, 76 (4): 438–443, doi:10.1007/bf01458215, ISSN 0025-5831, S2CID 121598654
^ Felix Hausdorff (2002), Egbert Brieskorn; Srishti D. Chatterji; et al. (eds.), Grundzüge der Mengenlehre (1. ed.), Berlin/Heidelberg: Springer, p. 587, ISBN3-540-42224-2 - Original edition (1914)
^ Cohen, Paul J. (December xv, 1963). "The Independence of the Continuum Hypothesis". Proceedings of the National Academy of Sciences of the United States of America. 50 (6): 1143–1148. Bibcode:1963PNAS...fifty.1143C. doi:x.1073/pnas.50.half-dozen.1143. JSTOR 71858. PMC221287. PMID 16578557.
^ Cohen, Paul J. (January 15, 1964). "The Independence of the Continuum Hypothesis, II". Proceedings of the National Academy of Sciences of the Usa. 51 (1): 105–110. Bibcode:1964PNAS...51..105C. doi:10.1073/pnas.51.1.105. JSTOR 72252. PMC300611. PMID 16591132.
^ Penrose, R (2005), The Road to Reality: A Complete guide to the Laws of the Universe, Vintage Books, ISBN0-09-944068-seven
^ Georg Cantor (1887), "Mitteilungen zur Lehre vom Transfiniten", Zeitschrift für Philosophie und philosophische Kritik, 91: 81–125
Reprinted in: Georg Cantor (1932), Adolf Fraenkel (Lebenslauf); Ernst Zermelo (eds.), Gesammelte Abhandlungen mathematischen und philosophischen Inhalts, Berlin: Springer, pp. 378–439 Here: p.413 lesser
^ Practical Abstruse Algebra, K.H. Kim, F.W. Roush, Ellis Horwood Series, 1983, ISBN 0-85312-612-seven (pupil edition), ISBN 0-85312-563-5 (library edition)

Source: https://en.wikipedia.org/wiki/Cardinality

Posted by: paulinoalonese.blogspot.com